What is Causal Inference?
Consider the following plot1:
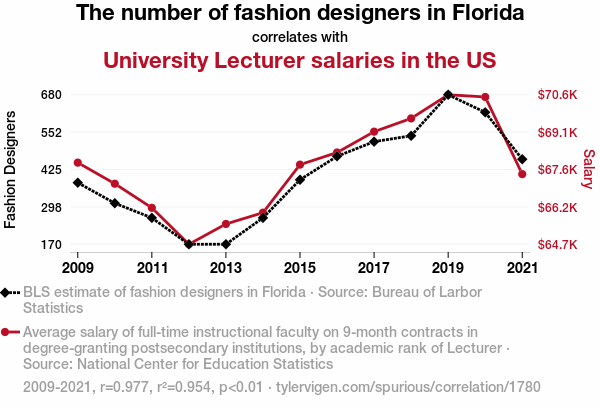
What is the reported correlation coefficient (\(r^2\)) value?
Go to the discussion board on Canvas and post a short (1–2 sentence) response explaining one possible reason for the trend shown in the graph. What might be driving this pattern? Your name will be hidden from other students.
Now read through the following AI-generated explanation for this observed trend with a high correlation:
“As more fashion designers flocked to Florida, it led to a surge in unique and flamboyant fashion trends. This created a sudden demand for expert fashion history and theory lecturers across the country. As universities scrambled to keep up with the latest haute couture curriculum, they had to offer higher salaries to attract and retain the most fashionable academic talent. So, in a twist no one saw coming, the Sunshine State’s affinity for style inadvertently elevated the bank accounts of university lecturers nationwide. After all, it’s not just the students who deserve a well-tailored education!”
Sounds a bit far-fetched, doesn’t it?
What we’re seeing here is a classic example of correlation not equaling causation — just because two things move together doesn’t mean one caused the other.
Causal inference is all about answering the question: What actually causes what? It’s the science of figuring out how one thing affects another—while carefully separating out confounders, factors that influence both variables and can make their causal relationship look misleading.
Explore more spurious correlations at this link.
In the next section, we will explore one powerful way to study causal relationships: randomized experiments.
Footnotes
Illustration and AI explanation with the prompt used to generate it can be found at Spurious Correlations.↩︎